Analytic manifold

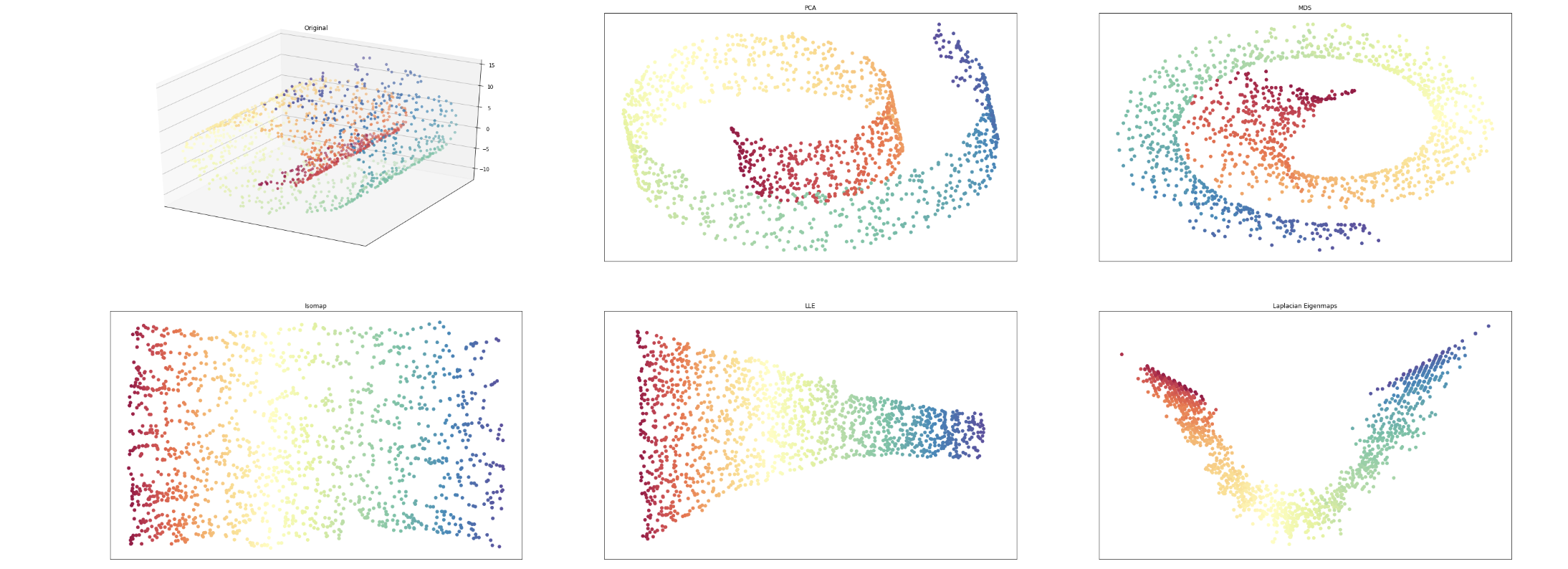
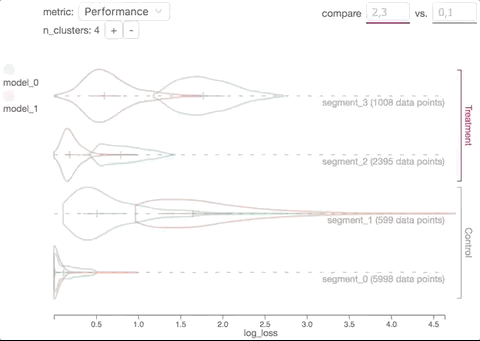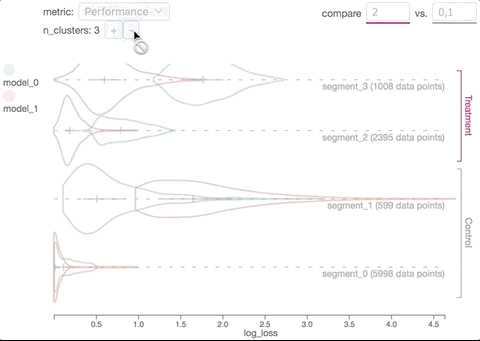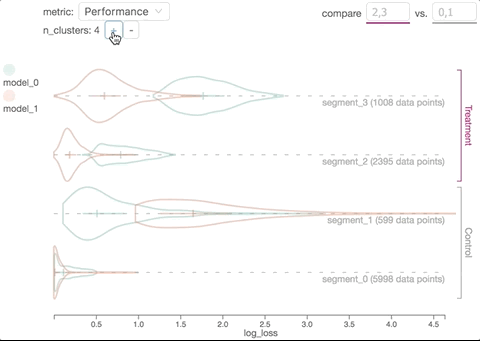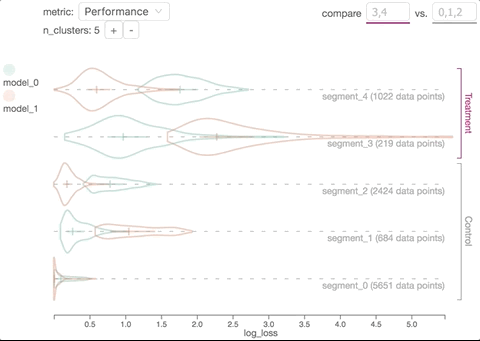
In mathematics, an analytic manifold, also known as a ${\displaystyle C^{\omega }}$ manifold, is a differentiable manifold with analytic transition maps. The term usually refers to real analytic manifolds, although complex manifolds are also analytic. In algebraic geometry, analytic spaces are a generalization of analytic manifolds such that singularities are permitted.

For ${\displaystyle U\subseteq \mathbb {R} ^{n}}$, the space of analytic functions, ${\displaystyle C^{\omega }(U)}$, consists of infinitely differentiable functions ${\displaystyle f:U\to \mathbb {R} }$, such that the Taylor series

$${\displaystyle T_{f}(\mathbf {x} )=\sum _{|\alpha |\geq 0}{\frac {D^{\alpha }f(\mathbf {x_{0}} )}{\alpha !}}(\mathbf {x} -\mathbf {x_{0}} )^{\alpha }}$$

converges to ${\displaystyle f(\mathbf {x} )}$ in a neighborhood of ${\displaystyle \mathbf {x_{0}} }$, for all ${\displaystyle \mathbf {x_{0}} \in U}$. The requirement that the transition maps be analytic is significantly more restrictive than that they be infinitely differentiable; the analytic manifolds are a proper subset of the smooth, i.e. ${\displaystyle C^{\infty }}$, manifolds. There are many similarities between the theory of analytic and smooth manifolds, but a critical difference is that analytic manifolds do not admit analytic partitions of unity, whereas smooth partitions of unity are an essential tool in the study of smooth manifolds. A fuller description of the definitions and general theory can be found at differentiable manifolds, for the real case, and at complex manifolds, for the complex case.

See also

• Complex manifold
• Analytic variety
• Algebraic geometry § Analytic geometry

References